Polarization Correction

The polarization correction is expected to be small at small angles, but it is deemed important.

\[I_{cor} = I_j \left[P (1 - (sin(\phi) sin(2\theta ))^2 ) (1 - P )(1 - (cos(\phi) sin(2\theta ))^2 )\right]\]

where \(\phi\) is the azimuthal angle on the detector surface (defined here clockwise, 0 at 12 o’clock) \(2\theta\) the scattering angle, and \(P\) the fraction of incident radiation polarized in the horizontal plane (azimuthal angle of \(90^{\circ}\)) The polarization correction is configured by two parameters in PolarizationCorrection. Its factors are included in the integration matrix (operator).

This input:

{
    "Geometry": {
        "Tilt": {
            "TiltAngleDeg": -0.56,
            "TiltRotDeg": 73.569
        },
        "DedectorDistanceMM": 1031.657,
        "BeamCenter": [
            808.37,
            387.772
        ],
        "Imagesize": [
            1043,
            981
        ],
        "PixelSizeMicroM": [
            172.0,
            172.0
        ]
    },
    "Directory": [
        "."
    ],
    "PolarizationCorrection": {
        "Angle": 0,
        "Fraction": 1
    },
    "Masks": [
        {
            "PixelPerRadialElement": 1,
            "MaskFile": "./data/AAA_integ.msk",
            "Oversampling": 2,
            "qStart": 0.0, 
            "qStop": 5.0
        }
    ],
    "Wavelength": 1.54
}

Gives:

(Source code, png, hires.png, pdf)

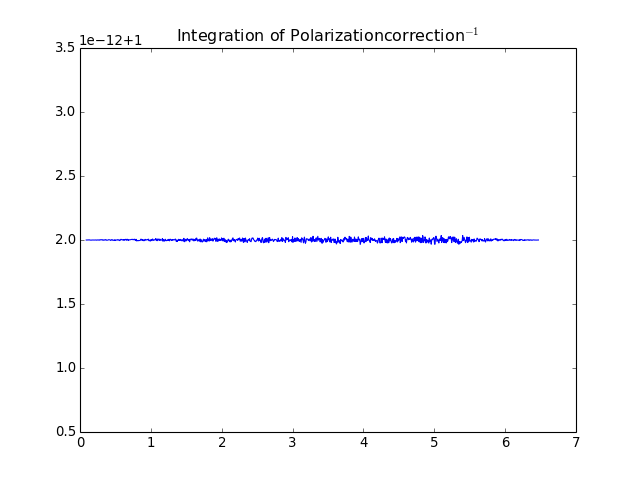
If the correction factors are all correctly in the algorithm, the integration of an image containing \(1/I_{corr}\) should give constant 1.0.

(Source code, png, hires.png, pdf)

Just for checking: integrating a picture with only ones gives something different:

(Source code, png, hires.png, pdf)

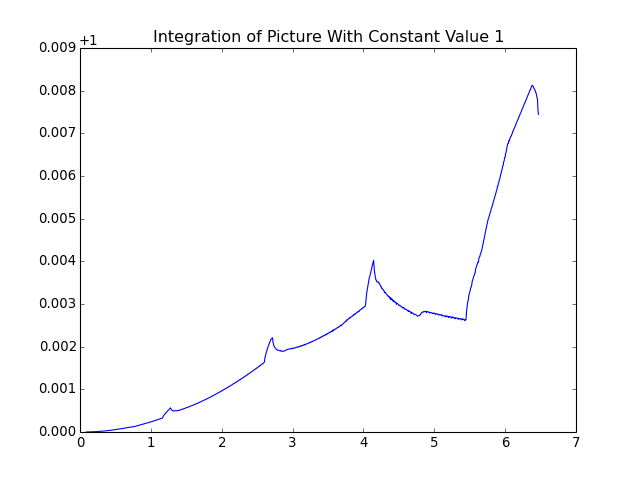
This are the wiggles that come from the polarization correction pattern